The Gold Model Revisited

Four years ago, I wrote a post discussing my thoughts on how to build a model for the price of gold. That post received by far the most attention of anything I’ve written. I still get emails about it today.

Over time, I’ve thought more about this issue, and I’ve altered my thinking somewhat. I also want to clarify some points from my original post. Instead of writing an addendum to it, though, I thought it would be clearer to rewrite the whole thing. What follows is the updated version.

******************************************************************

One of the most controversial topics in investing is the price of gold. Fifteen years ago, gold dropped as low as $252 per ounce. The yellow metal then enjoyed a furious rally as it soared above $1,920 per ounce, easily outpacing the major stock-market indexes. Over the last three years, however, it has sunk back down to $1,300.

Like Linus in the pumpkin patch waiting for the Great Pumpkin, many gold bugs hold out hope. They claim that any day now, gold will resume its march upward to $2,000, then $5,000 and then $10,000 per ounce. But my question is, “How can anyone reasonably calculate what the value of gold is?”

For stocks, we have all sorts of ratios. Sure, those ratios can be off, but at least they’re something. With gold, we have nothing. No assets or liabilities. Not even a dividend. After all, gold is just a rock (OK, OK, an element). How can we even begin to analyze gold’s value? There’s an old joke that the price of gold is understood by exactly two people in the entire world. They both work for the Bank of England, and they disagree.

In this post, I want to put forth a possible model for evaluating the price of gold. The purpose of the model isn’t to say where gold will go but to look at the underlying factors that drive the price of the precious metal. Let me caution you that as with any model, this one has its flaws, but that doesn’t mean it isn’t useful. More importantly, I’ll explain why our model makes theoretical sense, rather than just mashing up numbers and seeing what correlates.

The key to understanding the gold market is understanding that it’s not really about gold at all. Instead, it’s about currencies, and in our case that means the U.S. dollar. Properly understood, gold is really the anti-currency. It serves a valuable purpose in that it keeps all the other currencies honest—or exposes their dishonesty.

This may sound odd, but every major currency has an interest rate tied to it. It doesn’t matter if it’s the euro, the pound or the yen. In essence, that interest rate is what the currency is all about.

Before I get to my model, we need to take a slight detour and discuss a fascinating paradox known as Gibson’s Paradox. This is one the most puzzling topics in economics. Gibson’s Paradox is the observation that interest rates tend to follow the general price level and not the rate of inflation. That’s very strange, because it seems obvious that as inflation rises, interest rates ought to keep up. Similarly, as inflation falls back, rates should move back as well. But historically, that hasn’t been the case. Instead, interest rates have risen as prices have gone up, and only fallen when there’s been deflation.

This paradox has totally baffled economists for years. Yet it really does exist. John Maynard Keynes called it “one of the most completely established empirical facts in the whole field of quantitative economics.” Milton Friedman and Anna Schwartz said that “the Gibsonian Paradox remains an empirical phenomenon without a theoretical explanation.”

Even many of today’s prominent economists have tried to tackle Gibson’s Paradox. In 1977, Robert Shiller and Jeremy Siegel wrote a paper on the topic. In 1988 Robert Barsky and none other than Larry Summers took on the paradox in their paper “Gibson’s Paradox and the Gold Standard.” It’s this paper that I want to focus on. (By the way, in this paper the authors thank future econo-bloggers Greg Mankiw and Brad DeLong.)

Summers and Barsky agree that the Gibson Paradox does indeed exist. They also say that it’s not connected with nominal interest rates but with real (meaning after-inflation) interest rates. The catch is that the paradox only works under a gold standard. Absent that standard, the Gibson Paradox fades away.

Now here’s my big idea: the Gibson Paradox doesn’t go away. It’s still here, just harder to see. It’s my hypothesis that Summers and Barsky were on to something, and that we can use their insight to build a model for the price of gold. The key is that gold is tied to real interest rates. Where I differ from them is that I use real short-term interest rates, whereas they focused on long-term rates.

We’re getting closer to our model, but we need to take yet another detour, this time to Sweden to discuss the great Swedish economist Knut Wicksell. Wicksell was an interesting character who wrote on many topics, but he was deeply concerned with the theory of interest rates.

Now Wicksell was an economist, and consequently he wasn’t always the clearest writer. He often seemed to get his interest rates confused. One economist referred to this as the “Wicksellian muddle.” But what’s important is that Wicksell believed there was a constant tug-of-war between two interest rates. One is the interest you see in the real world, the money rate. The other is an invisible phantom rate called the natural rate. While unseen, this natural rate does make its presence known in various ways. Wicksell believed that when the money rate drops below the natural rate, the economy grows and prices rise. When the opposite happens, the economy contracts and prices fall.

I believe that if we take the Wicksellian natural rate and view it through the prism of a still-functioning Gibson’s Paradox, we can understand how gold’s value works.

Here’s what Wicksell wrote (page 102):

There is a certain rate of interest on loans which is neutral in respect to commodity prices, and tend neither to raise nor to lower them. This is necessarily the same as the rate of interest which would be determined by supply and demand if no use were made of money and all lending were effected in the form of real capital goods. It comes to much the same thing to describe it as the current value of the natural rate of interest on capital.

Bingo! It’s that natural rate that’s the key to our model. In the first iteration of my model, I used 2%. That was wrong, but I was fooled because 2% works well enough as a long-term approximation of the Wicksellian natural rate. But the natural rate is not a constant.

Here’s how it works. Whenever the dollar’s real short-term interest rate is below the Wicksellian natural rate, gold rallies. Whenever the real short-term rate is above the natural rate, then gold falls. Just as the Knut Man describes. When gold holds perfectly still, you know you’re at the natural rate. It’s my contention that this was what the Gibson Paradox was all about, since the price of gold is tied to the general price level.

Now we get to the messy parts. There’s a lot of volatility in this relationship. According to my original model, for every one percentage point real rates differ from the natural rate, gold moves by eight times that amount per year. So if the real rates are at 1% and the natural rate is at 2%, gold will move up at an 8% annualized rate. If real rates are 2% below the natural rate, then gold will move up at a 16% rate (that was about the story from 1999 to 2011). Conversely, if the real rate jumps to 1% above the natural rate, then gold will drop at an 8% rate.

Why eight fold? There, I don’t know. When I did the back test, that number fit the best. I assume it’s a risk factor to compensate for owning gold.

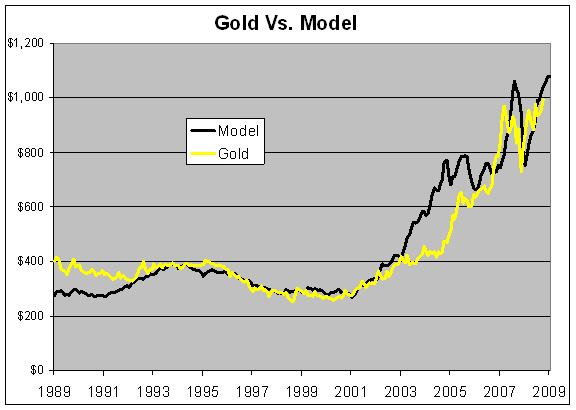
Here’s the graph from my original model, bearing in mind that I used 2% as the natural rates.

I realize I have a problem with using an unspecified Wicksellian natural interest rate, since I’m using one variable to explain another variable. That’s not quite kosher in the model-building biz. Perhaps I could use the price of gold and current interest rates to reverse-engineer the Wicksellian natural rate. Gold has been falling for the last three years, even though real short-term rates have been quite low. In fact, negative. The natural rate may have fallen as well.

Let me make it clear that this is just a model, and I’m not trying to explain 100% of gold’s movement. Gold is subject to a high degree of volatility and speculation. Geopolitical events, for example, can impact the price of gold. I would also imagine that at some point, gold could break a replacement price where it became so expensive that another commodity would replace its function in industry, and the price would suffer.

Instead of explaining every aspect of gold’s behavior, my aim is to pinpoint the underlying factors that are strongly correlated with it.

There are a few key takeaways.

The first and perhaps the most significant is that gold is not tied to inflation. It’s tied to low real rates, which are often the by-product of inflation. Rising gold and low inflation isn’t a contradiction. We had both for a few years.

The second point is that when real rates are low, the price of gold can rise very, very rapidly.

The third is that when real rates are high, gold can fall very, very quickly.

Fourth, there’s no reason for there to be a relationship between equity prices and gold (like the Dow-to-gold ratio).

The final point is that the price of gold is essentially political. If a central banker has the will to raise real rates as Volcker did 35 years ago, then the price of gold can be crushed.

(You can sign up for my free newsletter here.)

Posted by Eddy Elfenbein on July 24th, 2014 at 9:31 am

The information in this blog post represents my own opinions and does not contain a recommendation for any particular security or investment. I or my affiliates may hold positions or other interests in securities mentioned in the Blog, please see my Disclaimer page for my full disclaimer.